[인공지능]다층 퍼셉트론으로 XOR문제 해결하기

이 책에 있는 내용을 정리 한 것임. 

모두의 딥러닝 개정2판: 3 코딩으로 XOR 문제 해결하기 - 4

2 퍼셉트론의 과제

사람의 뇌가 작동하는 데 1,000억 개나 되는 뉴런이 존재해야 하는 이유는 하나의 뉴런만으로는 아무것도 할 수 없기 때문입니다. 퍼셉트론도 마찬가지입니다. 단 하나의 퍼셉트론으로는 많은 것을 기대할 수가 없습니다. 지금부터는 퍼셉트론의 한계와 이를 해결하는 과정을 보며 신경망의 기본 개념을 확립해 보겠습니다. 먼저 그림 6-2를 볼까요?

 

그림 6-2

사각형 종이에 놓인 검은점 두 개와 흰점 두 개

 

사각형 종이에 검은점 두 개와 흰점 두 개가 놓여 있습니다. 이 네 점 사이에 직선을 하나 긋는다고 합시다. 이때 직선의 한쪽 편에는 검은점만 있고, 다른 한쪽에는 흰점만 있게끔 선을 그을 수 있을까요?

 

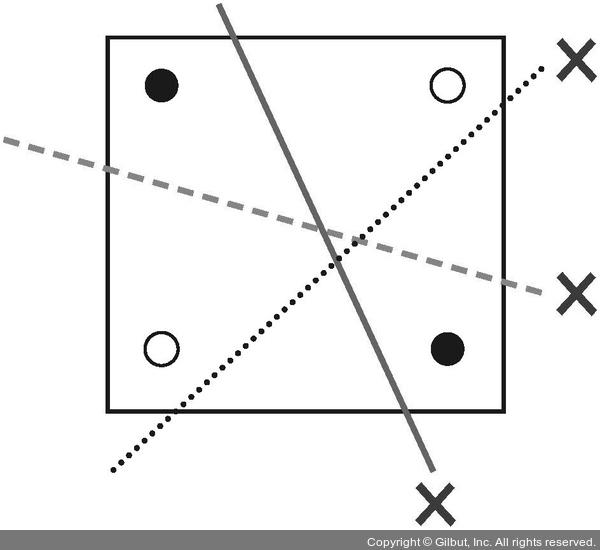
그림 6-3

선으로는 같은 색끼리 나눌 수 없다: 퍼셉트론의 한계

 

여러 개의 선을 아무리 그어보아도 하나의 직선으로는 흰점과 검은점을 구분할 수 없습니다.

앞서 배운 선형 회귀와 로지스틱 회귀를 통해 머신러닝이 결국 선이나 2차원 평면을 그리는 작업이란 것을 배웠습니다. 따라서 이와 같은 개념인 퍼셉트론 역시 선을 긋는 작업이라고 할 수 있습니다. 그런데 이 예시처럼 경우에 따라서는 선을 아무리 그어도 해결되지 않는 상황이 있습니다.

 

3 XOR 문제

 

이것이 퍼셉트론의 한계를 설명할 때 등장하는 XOR(exclusive OR) 문제입니다.

XOR 문제는 논리 회로에 등장하는 개념입니다. 컴퓨터는 두 가지의 디지털 값, 즉 0과 1을 입력해 하나의 값을 출력하는 회로가 모여 만들어지는데, 이 회로를 ‘게이트(gate)’라고 부릅니다.

표 6-1은 AND 게이트, OR 게이트 그리고 XOR 게이트에 대한 값을 정리한 것입니다. AND 게이트는 x1와 x2 둘 다 1일 때 결괏값이 1로 출력됩니다. OR 게이트는 둘 중 하나라도 1이면 결괏값이 1로 출력됩니다. XOR 게이트는 둘 중 하나만 1일 때 1이 출력됩니다.

 

AND 진리표			OR 진리표			XOR 진리표
x1	x2	결괏값	x1	x2	결괏값	x1	x2	결괏값
0	0	0	0	0	0	0	0	0
0	1	0	0	1	1	0	1	1
1	0	0	1	0	1	1	0	1
1	1	1	1	1	1	1	1	0

표 6-1

AND, OR, XOR 게이트에 대한 진리표

 

표 6-1을 각각 그래프로 좌표 평면에 나타내 보겠습니다. 결괏값이 0이면 흰점으로, 1이면 검은점으로 나타낸 후 조금 전처럼 직선을 그어 위 조건을 만족할 수 있는지 보겠습니다.

 

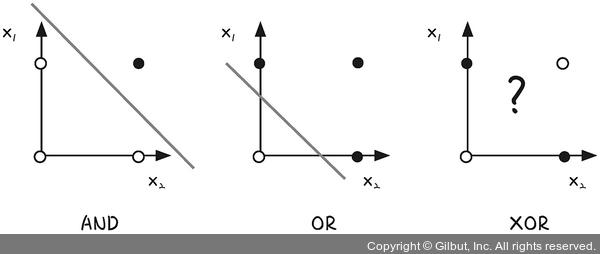
그림 6-4

AND, OR, XOR 진리표대로 좌표 평면에 표현한 뒤 선을 그어 색이 같은 점끼리 나누기(XOR은 불가능)

 

AND와 OR 게이트는 직선을 그어 결괏값이 1인 값(검은점)을 구별할 수 있습니다. 그러나 XOR의 경우 선을 그어 구분할 수 없습니다.

이는 인공지능 분야의 선구자였던 MIT의 마빈 민스키(Marvin Minsky) 교수가 1969년에 발표한 <퍼셉트론즈(Perceptrons)>라는 논문에 나오는 내용입니다. ‘뉴런 → 신경망 → 지능’이라는 도식을 따라 ‘퍼셉트론 → 인공 신경망 → 인공지능’이 가능하리라 꿈꾸던 당시 사람들은 이것이 생각처럼 쉽지 않다는 사실을 깨닫게 됩니다. 알고 보니 간단한 XOR 문제조차 해결할 수 없었던 것입니다. 이 논문 이후 인공지능 연구가 한동안 침체기를 겪게 됩니다. 10여 년이 지난 후에야 이 문제가 해결되는데, 이를 해결한 개념이 바로 다층 퍼셉트론(multilayer perceptron)입니다.

 

7장 다층 퍼셉트론

앞서 종이 위에 각각 엇갈려 놓인 검은점 두 개와 흰점 두 개를 하나의 선으로는 구별할 수 없다는 것을 살펴보았습니다. 언뜻 보기에 해답이 없어 보이는 이 문제를 해결하려면 새로운 접근이 필요합니다.

어릴 적 친구들에게 장난처럼 들었던 문제인데 의외로 기발한 해답에 기억에 오래 남는 것이 하나 있습니다. 바로 ‘성냥개비 여섯 개로 정삼각형 네 개를 만들 수 있는가’라는 문제였습니다.

 

그림 7-1

성냥개비 여섯 개로 정삼각형 네 개를?

 

골똘히 연구해도 답을 찾지 못했던 이 문제는 2차원 평면에서만 해결하려는 고정관념을 깨고 피라미드 모양으로 성냥개비를 쌓아 올리니 해결되었습니다.

 

그림 7-2

차원을 달리하니 쉽게 완성!

 

인공지능 학자들은 인공 신경망을 개발하기 위해서 반드시 XOR 문제를 극복해야만 했습니다. 이 문제 역시 고정관념을 깬 기발한 아이디어에서 해결점이 보였습니다. 그림 7-3은 전혀 새로운 방법으로 이를 해결하는 모습을 보여 줍니다.

 

그림 7-3

XOR 문제의 해결은 평면을 휘어주는 것!

 

로 종이를 휘어 주는 것이 답이었습니다. 즉, 좌표 평면 자체에 변화를 주는 것입니다. XOR 문제를 해결하기 위해서 우리는 두 개의 퍼셉트론을 한 번에 계산할 수 있어야 합니다. 이를 가능하게 하려면 숨어있는 층, 즉 은닉층(hidden layer)을 만들면 됩니다.

 

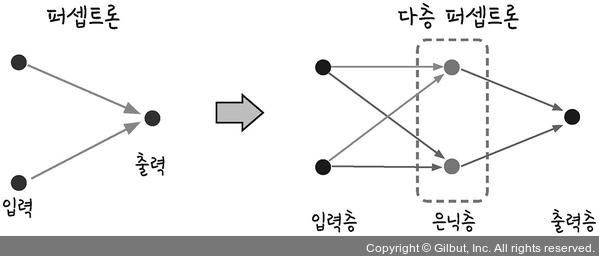
그림 7-4

퍼셉트론에서 다층 퍼셉트론으로

 

입력층과 은닉층의 그래프를 집어넣어 보면 그림 7-5와 같습니다. 은닉층이 좌표 평면을 왜곡시키는 결과를 가져옵니다.

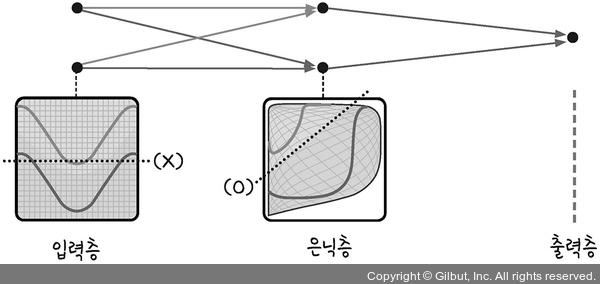
그림 7-5

은닉층의 공간 왜곡(https://goo.gl/8qEGHD 참조)

 

입력 값(input)을 놓고 파란색과 빨간색의 영역을 구분한다고 할 때, 그림 7-5의 왼쪽 그림을 보면 어떤 직선으로도 이를 해결할 수 없습니다. 하지만 은닉층을 만들어 공간을 왜곡하면 두 영역을 가로지르는 선이 직선으로 바뀝니다.

 

1 다층 퍼셉트론의 설계

 

다층 퍼셉트론이 입력층과 출력층 사이에 숨어있는 은닉층을 만드는 것을 도식으로 나타내면 그림 7-6과 같습니다.

 

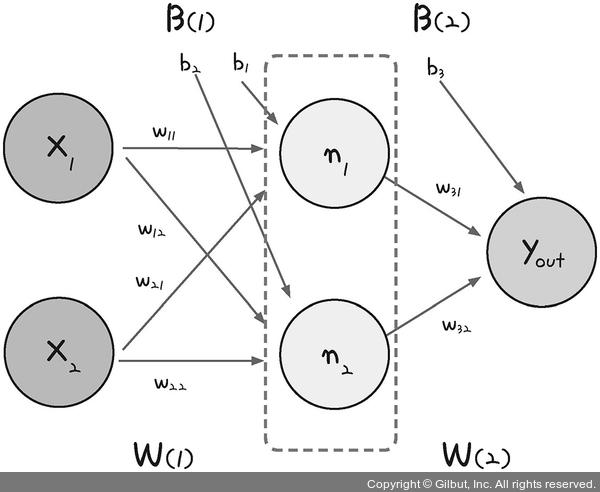
그림 7-6

다중 퍼셉트론의 내부

 

가운데 숨어있는 은닉층으로 퍼셉트론이 각각 자신의 가중치(w)와 바이어스(b) 값을 보내고, 이 은닉층에서 모인 값이 한 번 더 시그모이드 함수(기호로 σ라고 표시합니다)를 이용해 최종 값으로 결과를 보냅니다. 은닉층에 모이는 중간 정거장을 노드(node)라고 하며, 여기서는 n1과 n2로 표현하였습니다.

 

n1과 n2의 값은 각각 단일 퍼셉트론의 값과 같습니다.

 

n1 = σ(x1w11 + x2w21+b1)

n2 = σ(x1w12 + x2w22 + b2)

 

위 두 식의 결괏값이 출력층으로 보내집니다. 출력층에서는 역시 시그모이드 함수를 통해 y 값이 정해집니다. 이 값을 y out이라 할 때 식으로 표현하면 다음과 같습니다.

 

 

이제 각각의 가중치(w)와 바이어스(b)의 값을 정할 차례입니다. 2차원 배열로 늘어놓으면 다음과 같이 표시할 수 있습니다. 은닉층을 포함해 가중치 6개와 바이어스 3개가 필요합니다.

 

한 노드당 바이어스 하나를 주는구나..

 

2 XOR 문제의 해결

 

앞서 우리에게 어떤 가중치와 바이어스가 필요한지를 알아보았습니다. 이를 만족하는 가중치와 바이어스의 조합은 무수히 많습니다. 이를 구하는 방법은 8장에서 소개할 예정입니다. 지금은 먼저 다음과 같이 각 변숫값을 정하고 이를 이용해 XOR 문제를 해결하는 과정을 알아보겠습니다.

 

 

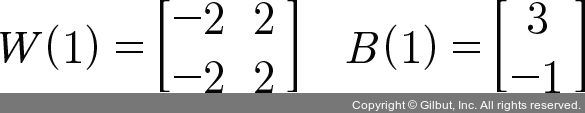
이것을 도식에 대입하면 다음과 같습니다.

 

그림 7-7

다중 퍼셉트론의 내부에 변수를 채워보자.

 

이제 x1의 값과 x2의 값을 각각 입력해 y 값이 우리가 원하는 값으로 나오는지를 점검해 보겠습니다.

 

x1	x2	n1	n2	yout	우리가 원하는 값
0	0	σ(0 * (-2) + 0 * (-2) + 3) ≈ 1	σ(0 * 2 + 0 * 2 - 1) ≈ 0	σ(1 * 1 + 0 * 1 - 1) ≈ 0	0
0	1	σ(0 * (-2) + 1 * (-2) + 3) ≈ 1	σ(0 * 2 + 1 * 2 - 1) ≈ 1	σ(1 * 1 + 1 * 1 - 1) ≈ 1	1
1	0	σ(1 * (-2) + 0 * (-2) + 3) ≈ 1	σ(1 * 2 + 0 * 2 - 1) ≈ 1	σ(1 * 1 + 1 * 1 - 1) ≈ 1	1
1	1	σ(1 * (-2) + 1 * (-2) + 3) ≈ 0	σ(1 * 2 + 1 * 2 - 1) ≈ 1	σ(0 * 1 + 1 * 1 - 1) ≈ 0	0

표 7-1

XOR 다층 문제 해결

 

TIP

≈ 기호는 ‘거의 같다’를 의미하는 것으로 이해하면 됩니다.

표 7-1에서 볼 수 있듯이 n1, n2, y를 구하는 공식에 차례로 대입하니 우리가 원하는 결과를 구할 수 있었습니다. 숨어있는 두 개의 노드를 둔 다층 퍼셉트론을 통해 XOR 문제가 해결된 것입니다.

 

3 코딩으로 XOR 문제 해결하기

 

이제 주어진 가중치와 바이어스를 이용해 XOR 문제를 해결하는 파이썬 코드를 작성해 볼까요?

먼저 표 7-1에서 n1의 값을 잘 보면 입력 값 x1, x2가 모두 1일 때 0을 출력하고 하나라도 0이 아니면 1을 출력하게 되어 있습니다. 이는 표 6-1에서 배운 AND 게이트의 정반대 값을 출력하는 방식입니다. 이를 NAND(Negative And) 게이트라고 부릅니다.

그리고 n2의 값을 잘 보면 x1, x2에 대한 OR 게이트에 대한 답입니다.

NAND 게이트와 OR 게이트, 이 두 가지를 내재한 각각의 퍼셉트론이 다중 레이어 안에서 각각 작동하고, 이 두 가지 값에 대해 AND 게이트를 수행한 값이 바로 우리가 구하고자 하는 Y_out임을 알 수 있습니다.

정해진 가중치와 바이어스를 numpy 라이브러리를 사용해 다음과 같이 선언하겠습니다.

import numpy as np
 
w11 = np.array([-2, -2])
w12 = np.array([2, 2])
w2 = np.array([1, 1])
b1 = 3
b2 = -1
b3 = -1

이제 퍼셉트론 함수를 만들어 줍니다. 0과 1 중에서 값을 출력하게 설정합니다.

def MLP(x, w, b):
    y = np.sum(w * x) + b
    if y <= 0:
        return 0
    else:
        return 1

각 게이트의 정의에 따라 NAND 게이트, OR 게이트, AND 게이트, XOR 게이트 함수를 만들어 줍니다.

# NAND 게이트
def NAND(x1, x2):
    return MLP(np.array([x1, x2]), w11, b1)
 
# OR 게이트
def OR(x1, x2):
    return MLP(np.array([x1, x2]), w12, b2)
 
# AND 게이트
def AND(x1, x2):
    return MLP(np.array([x1, x2]), w2, b3)
 
# XOR 게이트
def XOR(x1, x2):
    return AND(NAND(x1, x2),OR(x1, x2))

이제 x1과 x2 값을 번갈아 대입해 가며 최종 값을 출력해 봅시다.

if __name__ == '__main__':
    for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = XOR(x[0], x[1])
        print("입력 값: " + str(x) + " 출력 값: " + str(y))

모두 정리하면 다음과 같습니다.

import numpy as np
 
# 가중치와 바이어스
w11 = np.array([-2, -2])
w12 = np.array([2, 2])
w2 = np.array([1, 1])
b1 = 3
b2 = -1
b3 = -1
 
# 퍼셉트론
def MLP(x, w, b):
    y = np.sum(w * x) + b
    if y <= 0:
        return 0
    else:
        return 1
 
# NAND 게이트
def NAND(x1, x2):
    return MLP(np.array([x1, x2]), w11, b1)
 
# OR 게이트
def OR(x1, x2):
    return MLP(np.array([x1, x2]), w12, b2)
 
# AND 게이트
def AND(x1, x2):
    return MLP(np.array([x1, x2]), w2, b3)
 
# XOR 게이트
def XOR(x1, x2):
    return AND(NAND(x1, x2),OR(x1, x2))
 
# x1, x2 값을 번갈아 대입하며 최종값 출력
if __name__ == '__main__':
    for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = XOR(x[0], x[1])
        print("입력 값: " + str(x) + " 출력 값: " + str(y))

우리가 원하는 XOR 문제의 정답이 도출되었습니다.

이렇게 퍼셉트론 하나로 해결되지 않던 문제를 은닉층을 만들어 해결했습니다. 은닉층을 여러 개 쌓아올려 복잡한 문제를 해결하는 과정은 뉴런이 복잡한 과정을 거쳐 사고를 낳는 사람의 신경망을 닮았습니다. 그래서 이 방법을 ‘인공 신경망’이라 부르기 시작했고, 이를 간단히 줄여서 신경망이라고 통칭합니다.